Как определить нули функции по графику. Найдем нули функции. Основные свойства функций
В котором она принимает нулевое значение. Например, для функции , заданной формулой
Является нулём, поскольку
.Нули функции также называются корнями функции .
Понятие нулей функции можно рассматривать для любых функций, область значений которых содержит нуль или нулевой элемент соответствующей алгебраической структуры.
Для функции действительного переменного нулями являются значения, в которых график функции пересекает ось абсцисс .
Нахождение нулей функции часто требует использования численных методов (к примеру, метод Ньютона , градиентные методы).
Одной из нерешённых математических проблем является нахождение нулей дзета-функции Римана .
Корень многочлена
См. также
Литература
Wikimedia Foundation . 2010 .
Смотреть что такое "Нуль функции" в других словарях:
Точка, где заданная функция f (z) обращается в нуль; таким образом, Н. ф. f (z) это то же самое, что и корни уравнения f (z) = 0. Например, точки 0, π, π, 2π, 2π,... суть нули функции sinz. Нули аналитической функции (См. Аналитические… …
Нуль функция, нуль функции … Орфографический словарь-справочник
У этого термина существуют и другие значения, см. Нуль. Необходимо перенести содержимое этой статьи в статью «Нуль функции». Вы можете помочь проекту, объединив статьи. В случае необходимости обсуждения целесообразности объединения, замените этот … Википедия
Или C строка (от названия языка Си) или ASCIZ строка (от названия директивы ассемблера.asciz) способ представления строк в языках программирования, при котором вместо введения специального строкового типа используется массив символов, а концом… … Википедия
В квантовой теории поля принятое (жаргонное) название для свойства обращения в нуль фактора перенормировки константысвязи где g0 затравочная константа связи из лагранжиана взаимодействия, физ. константа связи, одетая взаимодействием. Равенство Z … Физическая энциклопедия
Нуль-мутация н-аллель - Нуль мутация, н. аллель * нуль мутацыя, н. алель * null mutation or n. allel or silent a. мутация, ведущая к полной потере функции в той последовательности ДНК, в которой она произошла … Генетика. Энциклопедический словарь
Утверждение в теории вероятностей о том, что всякое событие (т. н. остаточное событие), наступление к рого определяется лишь сколь угодно удаленными элементами последовательности независимых случайных событий или случайных величин, имеет… … Математическая энциклопедия
1) Число, обладающее тем свойством, что любое (действительное или комплексное) число при сложении с ним не меняется. Обозначается символом 0. Произведение любого числа на Н. равно Н.: Если произведение двух чисел равно Н., то один из сомножителей … Математическая энциклопедия
Функции, заданные соотношениями между независимыми переменными, не разрешенными относительно последних; эти соотношения являются одним из способов задания функции. Например, соотношение x2 + y2 1 = 0 задаёт Н. ф. … Большая советская энциклопедия
2. Найдем нули функции.
f(x) при х 
.
Ответ f(x) при х .
2) х 2 >-4x-5;
x 2 +4x +5>0;
Пусть f(x)=х 2 +4х +5 тогда Найдем такие х при которых f(x)>0,
D=-4 Нет нулей.
4. Системы неравенств. Неравенства и системы неравенств с двумя переменными
1) Множество решений системы неравенств есть пересечение множеств решений входящих в нее неравенств.
2) Множество решений неравенства f(х;у)>0 можно графически изобразить на координатной плоскости. Обычно линия, заданная уравнением f(х;у)=0 ,разбивает плоскость на 2 части, одна из которых является решением неравенства. Чтобы определить, какая из частей, надо подставить координаты произвольной точки М(х0;у0) , не лежащей на линии f(х;у)=0, в неравенство. Если f(х0;у0) > 0 , то решением неравенства является часть плоскости, содержащая точку М0. если f(х0;у0)<0, то другая часть плоскости.
3) Множество решений системы неравенств есть пересечение множеств решений входящих в нее неравенств. Пусть, например, задана система неравенств:
.
Для первого неравенства множество решений есть круг радиусом 2 и с центром в начале координат, а для второго- полуплоскость, расположенная над прямой 2х+3у=0. Множеством решений данной системы служит пересечение указанных множеств, т.е. полукруг.
4) Пример. Решить систему неравенств:
Решением 1-го неравенства служит множество , 2-го множество (2;7) и третьего - множество .
Пересечением указанных множеств является промежуток(2;3], который и есть множество решений системы неравенств.
5. Решение рациональных неравенств методом интервалов
В основе метода интервалов лежит следующее свойство двучлена (х-а): точка х=α делит числовую ось на две части - справа от точки α двучлен (х‑α)>0, а слева от точки α (х-α)<0.
Пусть требуется решить неравенство (x-α 1)(x-α 2)...(x-α n)>0, где α 1 , α 2 ...α n-1 , α n - фиксированные числа, среди которых нет равных, причем такие, что α 1 < α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 методом интервалов поступают следующим образом: на числовую ось наносят числа α 1 , α 2 ...α n-1 , α n ; в промежутке справа от наибольшего из них, т.е. числа α n , ставят знак «плюс», в следующем за ним справа налево интервале ставят знак «минус», затем - знак «плюс», затем знак «минус» и т.д. Тогда множество всех решений неравенства (x-α 1)(x‑α 2)...(x-α n)>0 будет объединение всех промежутков, в которых поставлен знак «плюс», а множество решений неравенства (x-α 1)(x-α 2)...(x‑α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».
1) Решение рациональных неравенств (т.е неравенств вида 
P(x) Q(x) где – многочлены) основано на следующем свойстве непрерывной функции: если непрерывная функция обращается в нуль в точках х1 и х2 (х1;х2) и между этими точками не имеет других корней, то в промежутках(х1;х2) функция сохраняет свой знак.
Поэтому для нахождения промежутков знакопостоянства функции y=f(x) на числовой прямой отмечают все точки, в которых функция f(x) обращается в нуль или терпит разрыв. Эти точки разбивают числовую прямую на несколько промежутков, внутри каждого из которых функция f(x) непрерывна и не обращается в нуль, т.е. сохраняет знак. Чтобы определить этот знак, достаточно найти знак функции в какой либо точке рассматриваемого промежутка числовой прямой.
2) Для определения интервалов знакопостоянства рациональной функции, т.е. Для решения рационального неравенства, отмечаем на числовой прямой корни числителя и корни знаменателя, которые как и являются корнями и точками разрыва рациональной функции.
Решение неравенств методом интервалов
3. 
< 20.
Решение. Область допустимых значений определяется системой неравенств:
Для функции f(x) = – 20. Находим f(x):
откуда x = 29 и x = 13.
f(30) = – 20 = 0,3 > 0,
f(5) = – 1 – 20 = – 10 < 0.
Ответ: . Основные методы решения рациональных уравнений. 1) Простейшие: решаются путём обычных упрощений - приведение к общему знаменателю, приведение подобных членов и так далее. Квадратные уравнения ax2 + bx + c = 0 решаются по...
X изменяется на промежутке (0,1], и убывает на промежутке .
Мы видим, что добавление n к аргументу x , не меняет
значение функции. Наименьшее отличное от нуля число
из n есть , таким образом, это период sin 2 x .
Нули функции. Значение аргумента, при котором функция равна 0, называется нулём ( корнем) функции . Функция может иметь несколько нулей. Например, функция y = x (x + 1) (x — 3) имеет три нуля: x = 0, x = — 1, x = 3. Геометрически нуль функции – это абсцисса точки пересечения графика функции с осью Х .
На рис.7 представлен график функции с нулями: x = a , x = b и x = c .
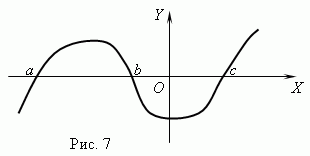
Асимптота. Если график функции неограниченно приближается к некоторой прямой при своём удалении от начала координат, то эта прямая называется асимптотой .
Тема 6. «Метод интервалов».
Если f (x) f (x 0) при х х 0 , то функцию f (x) называют непрерывной в точке х 0 .
Если функция непрерывна в каждой точке некоторого промежутка I , то ее называют непрерывной на промежутке I (промежуток I называют промежутком непрерывности функции ). График функции на этом промежутке представляет собой непрерывную линию, о которой говорят, что ее можно «нарисовать, не отрывая карандаша от бумаги».
Свойство непрерывных функций.
Если на интервале (a ; b) функция f непрерывна и не обращается в нуль, то она на этом интервале сохраняет постоянный знак.
На этом свойстве основан метод решения неравенств с одной переменной – метод интервалов. Пусть функция f(x) непрерывна на интервале I и обращается в нуль в конечном числе точек этого интервала. По свойству непрерывных функций этими точками I разбивается на интервалы, в каждом из которых непрерывная функция f(x) c охраняет постоянный знак. Чтобы определить этот знак, достаточно вычислить значение функции f(x) в какой-либо одной точке из каждого такого интервала. Исходя из этого, получим следующий алгоритм решения неравенств методом интервалов.
Метод интервалов для неравенств вида
Метод интервалов. Средний уровень.
Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?
Линейная функция
Линейной называется функция вида. Рассмотрим для примера функцию. Она положительна при 3″> и отрицательна при. Точка – нуль функции (). Покажем знаки этой функции на числовой оси:
Говорим, что «функция меняет знак при переходе через точку ».
Видно, что знаки функции соответствуют положению графика функции: если график выше оси, знак « », если ниже – « ».
Если обобщить полученное правило на произвольную линейную функцию, получим такой алгоритм:
Квадратичная функция
Надеюсь, ты помнишь, как решаются квадратные неравенства? Если нет, прочти тему «Квадратные неравенства». Напомню общий вид квадратичной функции: .
Теперь вспомним, какие знаки принимает квадратичная функция. Ее график – парабола, и функция принимает знак « » при таких, при которых парабола выше оси, и « » – если парабола ниже оси:
Если у функции есть нули (значения, при которых), парабола пересекает ось в двух точках – корнях соответствующего квадратного уравнения. Таким образом ось разбивается на три интервала, а знаки функции попеременно меняются при переходе через каждый корень.
А можно ли как-нибудь определить знаки, не рисуя каждый раз параболу?
Вспомним, что квадратный трехчлен можно разложить на множители:
Отметим корни на оси:
Мы помним, что знак функции может меняться только при переходе через корень. Используем этот факт: для каждого из трех интервалов, на которые ось разбивается корнями, достаточно определить знак функции только в одной произвольно выбранной точке: в остальных точках интервала знак будет таким же.
В нашем примере: при 3″> оба выражения в скобках положительны (подставим, например: 0″>). Ставим на оси знак « »:
Ну и, при (подставь, например,) обе скобки отрицательны, значит, произведение положительно:
Это и есть метод интервалов : зная знаки сомножителей на каждом интервале, определяем знак всего произведения.
Рассмотрим также случаи, когда нулей у функции нет, или он всего один.
Если их нет, то и корней нет. А значит, не будет и «перехода через корень». А значит, функция на всей числовой оси принимает только один знак. Его легко определить, подставив в функцию.
Если корень только один, парабола касается оси, поэтому знак функции не меняется при переходе через корень. Какое правило придумаем для таких ситуаций?
Если разложить такую функцию на множители, получатся два одинаковых множителя:
А любое выражение в квадрате неотрицательно! Поэтому знак функции и не меняется. В таких случаях будем выделять корень, при переходе через который знак не меняется, обведя его квадратиком:
Такой корень будем называть кратным .
Метод интервалов в неравенствах
Теперь любое квадратное неравенство можно решать без рисования параболы. Достаточно только расставить на оси знаки квадратичной функции, и выбрать интервалы в зависимости от знака неравенства. Например:
Отмерим корни на оси и расставим знаки:
Нам нужна часть оси со знаком « »; так как неравенство нестрогое, сами корни тоже включаются в решение:
Теперь рассмотрим рациональное неравенство – неравенство, обе части которого являются рациональными выражениями (см. «Рациональные уравнения»).
Пример:
Все множители кроме одного – – здесь «линейные», то есть, содержат переменную только в первой степени. Такие линейные множители нам и нужны для применения метода интервалов – знак при переходе через их корни меняется. А вот множитель вообще не имеет корней. Это значит, что он всегда положительный (проверь это сам), и поэтому не влияет на знак всего неравенства. Значит, на него можно поделить левую и правую часть неравенства, и таким образом избавиться от него:
Теперь все так же, как было с квадратными неравенствами: определяем, в каких точках каждый из множителей обращается в нуль, отмечаем эти точки на оси и расставляем знаки. Обращаю внимание очень важный факт:
В случае четного количества поступаем так же, как и раньше: обводим точку квадратиком и не меняем знак при переходе через корень. А вот в случае нечетного количества это правило не выполняется: знак все-равно поменяется при переходе через корень. Поэтому с таким корнем ничего дополнительно не делаем, как будто он у нас не кратный. Вышеописанные правила относятся ко всем четным и нечетным степеням.
Что запишем в ответе?
При нарушении чередования знаков нужно быть очень внимательным, ведь при нестрогом неравенстве в ответ должны войти все закрашенные точки . Но некоторые из нах часто стоят особняком, то есть не входят в закрашенную область. В этом случае мы добавляем их к ответу как изолированные точки (в фигурных скобках):
Примеры (реши сам):
Ответы:
- Если среди множителей просто – это корень, ведь его можно представить как.
.
Значения аргумента z при которыхf (z ) обращается в ноль наз. нулевой точкой , т.е. если f (a ) = 0 , то а - нулевая точка .
Опр.
Точка а
наз. нулём
порядка
n
, если
ФКП можно
представить в виде f
(z
)
=
,
где
аналитическая функция и
0.
В этом случае в разложении функции в ряд Тейлора (43) первые n коэффициентов равны нулю
=
=
Пр.
Определить порядок нуля для
и (1 –cos
z
)
при z
=
0
=
=
ноль 1 порядка
1
– cos
z
=
=
ноль 2 порядка
Опр.
Точка z
=
наз. бесконечно
удаленной точкой
и
нулем
функции
f
(z
),
если f
(
)
= 0. Такая функция разлагается в ряд по
отрицательным степеням z
: f
(z
)
=
.
Если
первые
n
коэффициентов
равны нулю, то приходим к нулю
порядка
n
в бесконечно
удаленной точке: f
(z
)
= z
-
n
.
Изолированные особые точки делятся на: а) устранимые особые точки ; б) полюса порядка n ; в) существенно особые точки .
Точка
а
наз. устранимой
особой точкой
функции
f
(z
)
, если при z
a
lim
f
(z
)
= с -
конечное число .
Точка
а
наз. полюсом
порядка
n
(n
1)
функции f
(z
),
если обратная функция
=
1/
f
(z
)
имеет нуль порядка n
в точке а.
Такую функцию
всегда можно представить в виде f
(z
)
=
,
где
-
аналитическая функция и
.
Точка
а
наз. существенно
особой точкой
функции
f
(z
),
если при z
a
lim
f
(z
)
не существует.
Ряд Лорана
Рассмотрим случай кольцевой области сходимости r < | z 0 – a | < R с центром в точке а для функции f (z ). Введем две новые окружности L 1 (r ) и L 2 (R ) вблизи границ кольца с точкой z 0 между ними. Сделаем разрез кольца, по кромкам разреза соединим окружности, перейдем к односвязной области и в
интегральной формуле Коши (39) получим два интеграла по переменной z
f
(z
0)
=
+
,
(42)
где интегрирование идет в противоположных направлениях.
Для интеграла по L 1 выполняется условие | z 0 – a | > | z – a |, а для интеграла по L 2 обратное условие | z 0 – a | < | z – a |. Поэтому множитель 1/(z – z 0) разложим в ряд (а) в интеграле по L 2 и в ряд (b) в интеграле по L 1 . В результате получаем разложение f (z ) в кольцевой области в ряд Лорана по положительным и отрицательным степеням (z 0 – a )
f
(z
0)
=
A
n
(z
0
– a
) n
(43)
где
A
n
=
=
;A
-n
=
Разложение по положительным степеням (z 0 – а )наз. правильной частью ряда Лорана (ряд Тейлора), а разложение по отрицательным степеням наз. главной частью ряда Лорана.
Если внутри круга L 1 нет особых точек и функция аналитична, то в (44) первый интеграл равен нулю по теореме Коши и в разложении функции останется только правильная часть. Отрицательные степени в разложении (45) появляются лишь при нарушении аналитичности в пределах внутреннего круга и служат для описания функции вблизи изолированных особых точек.
Для построения ряда Лорана (45) для f (z ) можно вычислять коэффициенты разложения по общей формуле или использовать разложения элементарных функций, входящих в f (z ).
Число
слагаемых (n
)
главной части ряда Лорана зависит от
типа особой точки: устранимая
особая точка
(n
=
0)
; существенно
особая точка
(n
);
полюс
n
– ого порядка
(n
-
конечное
число).
а)
Для f
(z
)
=
точка z
= 0 устранимая
особая точка,
т.к.
главной части нет. f
(z
)
=
(z
-
) = 1 -
б)
Для f
(z
)
=
точка z
= 0 -
полюс 1 – ого порядка
f
(z
)
=
(z
-
) =
-
с) Для f (z ) = e 1 / z точка z = 0 - существенно особая точка
f
(z
)
=
e
1 /
z
=
Если
f
(z
)
аналитична в области D
за исключением m
изолированных особых точек
и |z
1 |
< |z
2 |
< . . . < |z
m
|
, то при разложении функции по степеням
z
вся плоскость разбивается на m
+ 1 кольцо | z
i
|
< | z
| < | z
i
+ 1 |
и ряд Лорана имеет разный вид для
каждого кольца. При разложении по
степеням (z
–
z
i
) областью
сходимости ряда Лорана является круг
| z
–
z
i
| < r
,
где r
– расстояние
до ближайшей особой точки.
Пр.
Разложим функцию f
(z
)
=
в ряд Лорана по степенямz
и (z
-
1).
Решение.
Представим функцию в виде f
(z
)
= - z
2
.
Используем формулу для суммы геометрической
прогрессии
.
В круге |z|
< 1 ряд сходится и f
(z
)
= - z
2
(1 + z
+ z
2
+ z
3
+ z
4
+ . . .) = - z
2
- z
3
- z
4
- . . . , т.е. разложение содержит только
правильную
часть. Перейдем во внешнюю область
круга |z|
> 1 . Функцию представим в виде
, где 1/|z
|
< 1, и получим разложение f
(z
)
= z
=z
+ 1 +
Т.к.
,
разложение функции по степеням (z
-
1) имеет вид
f
(z
)
= (z
-
1) -1
+ 2 + (z
-
1) для всех
1.
Пр.
Разложить в ряд Лорана функцию f
(z
)
=
:
а)по степеням
z
в круге |z
|
< 1; b)
по степеням z
кольце 1 <
|z
|
< 3 ; c)
по степеням (z
–
2).Решение.
Разложим функцию на простейшие дроби
=
=
+
=
.
Из условий
z
=1
A
= -1/2 , z
=3
B
= ½.
а)
f
(z
)
=
½ [
]
= ½ [
-(1/3)
],
при |z
|<
1.
b)
f
(z
)
= - ½ [
+
]
= -
(
),
при 1 < |z
|
< 3.
с)
f
(z
)
=
½ [
]= -
½
[
]
=
=
- ½
= -
, при |2 - z
|
< 1
Это круг радиуса 1 с центром в точке z = 2 .
В ряде случаев степенные ряды можно свести к набору геометрических прогрессий и после этого легко определить область их сходимости.
Пр. Исследовать сходимость ряда
.
. . +
+
+
+
1
+ ()
+ ()
2
+ ()
3
+ . . .
Решение.
Это сумма двух геометрических прогрессий
с q
1
=
, q
2
= ()
. Из условий их сходимости следует
< 1 ,
< 1 или |z
|
> 1 , |z
|
< 2 , т.е. область сходимости ряда кольцо
1 < |z
|
< 2 .
