Элементарное преобразование строк. Элементарные матрицы. Методы решения систем линейных уравнений

Элементарн ыми преобразованиями строк матрицы называется преобразования следующих типов:

1) Умножение каждого элемента некоторой строки на одно и то же ненулевое число. Остальные строки остаются без изменения (кратко: умножение строки на число).

2) Прибавление к каждому элементу некоторой строки соответствующих элементов другой строки, умноженные на одно и то же число. Остальные строки (в том числе и прибавляемое) остаются без изменения (кратко: прибавление к строке другой, умноженной на число).

3) Перемена местами некоторых двух строк матрицы. Остальные строки остаются без изменения.

Эти преобразования называются соответственно преобразованиями первого , второго и третьеготипа (рода ). Последовательно применяя их, мы получаем более сложные преобразования.

Аналогично определяются элементарные преобразования столбцов матрицы.

Теорема

Преобразование третьего типа является некоторой комбинацией преобразований первого и второго типов .

Таким образом, преобразованием третьего типа можно отнести к более сложным, чем элементарные. Но его принято всё-же считать элементарным ради удобства.

Теорема

Любую матрицу элементарными преобразованиями строк можно привести к ступенчатой . Если к матрице применить элементарные преобразования строк и столбцов , то её можно привести к трапециедальному виду .

Например ,

á(1) Поменяли местами первую и вторую строки (преобразование третьего типа).

(2) Первую строку, умноженную на 2, прибавили ко второй и вычли из третьей, умноженную на 3, прибавили к четвёртой (преобразования второго типа).

(3) Вторую строку вычли из третьей и вторую строку, умноженную на 14/11 вычли из четвёртой.

(4) Поменяли местами третью и четвёртую строки.ñ

Таким образом, преобразовали исходную матрицу

в ступенчатую

Теперь, поменяв местами второй и третий столбец, а затем поменяв его же с четвёртым столбцом, перемещаем второй столбец на место четвёртого, третий и четвёртый столбцы окажутся соответственно на месте второго и третьего столбцов:

тем самым преобразовали исходную матрицу в трапециедальную.

Упражнения

Привести матрицу к ступенчатому и трапециедальному видам:

Определение 5.8. Элементарными преобразованиями строк матрицы называют следующие преобразования:

1) умножение строки матрицы на ненулевое действительное число;

2) прибавление к одной строке матрицы другой её строки, умноженной на произвольное действительное число.

Лемма 5.1. С помощью элементарных преобразований строк матрицы можно поменять местами любые две строки.

Доказательство.

А= .

.

Ступенчатая матрица. Ранг матрицы

Определение 5.9. Ступенчатой будем называть матрицу, которая обладает следующими свойствами:

1) если i -я строка нулевая, то (i + 1)-я строка также нулевая,

2) если первые ненулевые элементы i -й и (i + 1)-й строк расположены в столбцах с номерами k и R , соответственно, то k < R .

Условие 2) требует обязательного увеличения нулей слева при переходе от i -й строки к (i + 1)-й строке. Например, матрицы

А 1 = , А 2 = , А 3 =

являются ступенчатыми, а матрицы

В 1 = , В 2 = , В 3 =

ступенчатыми не являются.

Теорема 5.1. Любую матрицу можно привести к ступенчатой с помощью элементарных преобразований строк.

Проиллюстрируем эту теорему на примере.

А =

.

Получившаяся матрица – ступенчатая.

Определение 5.10. Рангом матрицы будем называть число ненулевых строк в ступенчатом виде этой матрицы.

Например, ранг матрицы А в предыдущем примере равен 3.

Вопросы для самоконтроля

1. Что называется матрицей?

2. Как производится сложение и вычитание матриц; умножение матрицы на число?

3. Дайте определение умножению матриц.

4. Какая матрица называется транспонированной?

5. Какие преобразования строк матрицы называются элементарными?

6. Дайте определение ступенчатой матрицы.

7. Что называют рангом матрицы?

Определители

Вычисление определителей

Определители второго порядка

Рассмотрим квадратную матрицу второго порядка

Определение 6.1. Определителем второго порядка, соответствующим матрице A,называется число, вычисляемое по формуле

│А │= = .

Элементы a ij называются элементами определителя │A │, элементы а 11 , а 22 образуют главную диагональ , а элементы а 12 , а 21 – побочную.

Пример. = –28 + 6 = –22.

Определители третьего порядка

Рассмотрим квадратную матрицу третьего порядка

А = .

Определение 6.2. Определителем третьего порядка, соответствующим матрице А , называется число, вычисляемое по формуле

│А │= = .

Чтобы запомнить, какие произведения в правой части равенства следует брать со знаком «плюс», а какие ─ со знаком «минус», полезно запомнить правило, называемое правилом треугольника:

Пример.

1) = –4 + 0 + 4 – 0 + 2 + 6 = 8.

2) = 1, т. е. │Е 3 │= 1.

Рассмотрим ещё один способ вычисления определителя третьего порядка.

Определение 6.3. Минором M ij элемента a ij определителя называется определитель, полученный из данного вычёркиванием i -й строки и j -го столбца. Алгебраическим дополнением A ij элемента a ij определителя называется его минор M ij , взятый со знаком (–1) i + j .

Пример. Вычислим минор М 23 и алгебраическое дополнение А 23 элемента а 23 в матрице

Вычислим минор М 23:

М 23 = = = –6 + 4 = –2.

Тогда А 23 = (–1) 2+3 М 23 = 2.

Теорема 6.1. Определитель третьего порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.

Доказательство. По определению

= . (6.1)

Выберем, например, вторую строку и найдём алгебраически дополнения А 21 , А 22 , А 23:

А 21 = (–1) 2+1 = –() = ,

А 22 = (–1) 2+2 = ,

А 23 = (–1) 2+3 = –() = .

Преобразуем теперь формулу (6.1)

│А │= () + () + () =

= А 21 + А 22 + А 23.

Формула А │= А 21 + А 22 + А 23 . называется разложением определителя │А │ по элементам второй строки. Аналогично разложение можно получить по элементам других строк и любого столбца

Пример.

= (по элементам второго столбца) = 1× (–1) 1+2 + 2 × (–1) 2+2 +

+ (–1)(–1) 3+2 = –(0 + 15) + 2(–2 +20) + (–6 +0) = –15 +36 – 6 = 15.

6.1.3 Определители n-го порядка (n N )

Определение 6.4. Определителем n -го порядка, соответствующим матрице n -го порядка

А =

называется число, равное сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения, т. е.

│A │= А i1 + A i2 + … + A in = А 1j + A 2j + … + A nj .

Нетрудно заметить, что при n = 2 получается формула для вычисления определителя второго порядка. Если n = 1, то по определению будем считать |A | = |a | = a .

Пример. = (по элементам 4-й строки) = 3×(–1) 4+2 +

2×(–1) 4+4 = 3(–6 + 20 –2 –32) +2(– 6 +16 +60 +2) = 3(–20) +2×72 = –60 +144 = 84.

Заметим, что если в определителе все элементы какой-либо строки (столбца), кроме одного, равны нулю, то при вычислении определителя его удобно разложить по элементам этой строки (столбца).

Пример.

│Е n │= = 1 × │E n - 1 │ = … = │E 3 │= 1.

Свойство определителей

Определение 6.5. Матрицу вида

или

будем называть треугольной матрицей.

Свойство 6.1. Определитель треугольной матрицы равен произведению элементов главной диагонали, т. е.

= = .

Свойство 6.2. Определитель матрицы с нулевой строкой или нулевым столбцом равен нулю.

Свойство 6.3. При транспонировании матрицы определитель не изменяется, т. е.

│А │= │А t │.

Свойство 6.4. Если матрица В получается из матрицы А умножением каждого элемента некоторой строки на число k , то

│В │= k │А │.

Свойство 6.5.

= + .

Свойство 6.6. Если матрица В получается из матрицы А перестановкой двух строк, то│В │= −│А │.

Свойство 6.7. Определитель матрицы с пропорциональными строками равен нулю, в частности, нулю равен определитель матрицы с двумя одинаковыми строками.

Свойство 6.8. Определитель матрицы не изменяется, если к элементам одной строки прибавить элементы другой строки матрицы, умноженные на некоторое число.

Замечание. 6.1. Так, как по свойству 6.3 определитель матрицы не меняется при транспонировании, то все свойства о строках матрицы верны и для столбцов.

Свойство 6.9. Если А и В – квадратные матрицы порядка n , то │АВ │=│А ││В │.

Обратная матрица

Определение 6.6. Квадратная матрица А порядка n называется обратимой, если существует матрица В такая, что АВ = ВА = Е n . В этом случае матрица В называется обратной к матрице А и обозначается А –1 .

Теорема 6.2. Справедливы следующие утверждения:

1) если матрица А обратима, то существует точно одна ей обратная матрица;

2) обратимая матрица имеет определитель, отличный от нуля;

3) если А и В – обратимые матрицы порядка n , то матрица АВ обратима, причём (АВ ) –1 = В –1 ×А –1 .

Доказательство.

1. Пусть В и С – матрицы, обратные к матрице А , т. е. АВ = ВА = Е n и АС = СА = Е n . Тогда В = ВЕ n = В (АС ) = (ВА )С = Е n С = С .

2. Пусть матрица А обратима. Тогда существует матрица А –1 , ей обратная, причём

АА –1 = Е n .

По свойству 6.9 определителя │АА –1 │=│А ││А –1 │. Тогда │А ││А –1 │=│Е n │, откуда │А ││А –1 │= 1. Следовательно, │А │¹ 0.

3. Действительно,

(АВ )(В –1 А –1) = (А (ВВ –1))А –1 = (АЕ n )А –1 = АА –1 = Е n .

(В –1 А –1)(АВ ) = (В –1 (А –1 А 21 = –1, А 22 = 2. Тогда А –1 = .

Вопросы для самоконтроля

1. Что называется определителем?

2. Каковы его основные свойства?

3. Что называется минором и алгебраическим дополнением?

4. Каковы способы вычисления определителей (второго, третьего и n -го порядков)?

5. Какая матрица называется квадратной?

Похожая информация.

К элементарным преобразованиям матрицы относятся:

1. Изменение порядка строк (столбцов).

2. Отбрасывание нулевых строк (столбцов).

3. Умножение элементов любой строки (столбца) на одно число.

4. Прибавление к элементам любой строки (столбца) элементов другой строки (столбца), умноженных на одно число.

Системы линейных алгебраических уравнений слу (Основные понятия и определения).

1. Системой m линейных уравнений с n неизвестными называется система уравнений вида:

2. Решением системы уравнений (1) называется совокупность чисел x 1 , x 2 , … , x n , обращающая каждое уравнение системы в тождество.

3. Система уравнений (1) называется совместной , если она имеет хотя бы одно решение; если система не имеет решений, она называется несовместной .

4. Система уравнений (1) называется определенной , если она имеет только одно решение, и неопределенной , если у нее более одного решения.

5. В результате элементарных преобразований система (1) преобразуется к равносильной ей системе (т.е. имеющей то же множество решений).

К элементарным преобразованиям систем линейных уравнений относятся:

1. Отбрасывание нулевых строк.

2. Изменение порядка строк.

3. Прибавление к элементам любой строки элементов другой строки, умноженных на одно число.

Методы решения систем линейных уравнений.

1) Метод обратной матрицы (матричный метод) решения систем n линейных уравнений с n неизвестными.

Системой n линейных уравнений с n неизвестными называется система уравнений вида:

Запишем систему (2) в матричном виде, для этого введем обозначения.

Матрица коэффициентов перед переменными:

X = ‒ матрица переменных.

В = ‒ матрица свободных членов.

Тогда система (2) примет вид:

A ×X = B ‒ матричное уравнение.

Решив уравнение, получим:

X = A -1 ×B

Пример:

; ;

1) │А│= 15 + 8 ‒18 ‒9 ‒12 + 20 = 4  0 матрицаА -1 существует.

3)

à =

4) А -1 = × Ã =;

Х = А -1 × B

Ответ:

2) Правило Крамера решения систем n – линейных уравнений с n – неизвестными.

Рассмотрим систему 2 ‒ х линейных уравнений с 2 ‒ мя неизвестными:

Решим эту систему методом подстановки:

Из первого уравнения следует:

Подставив во второе уравнение, получим:

Подставляем значение в формулу для, получим:

Определитель Δ - определитель матрицы системы;

Δ x 1 - определитель переменной x 1 ;

Δ x 2 - определитель переменной x 2 ;

Формулы:

x 1 =;x 2 =;…,x n = ;Δ  0;

‒ называются формулами Крамера.

При нахождении определителей неизвестных х 1 , х 2 ,…, х n заменяется столбец коэффициентов при той переменной, определитель которой находят, на столбец свободных членов.

Пример: Решить систему уравнений методом Крамера

Решение:

Составим и вычислим сначала главный определитель этой системы:

Так как Δ ≠ 0, то система имеет единственное решение, которое можно найти по правилу Крамера:

где Δ 1 , Δ 2 , Δ 3 получаются из определителя Δ путем замены 1‒ го, 2 ‒ го или 3 ‒ го столбца, соответственно, на столбец свободных членов.

Таким образом:

Метод Гаусса решения систем линейных уравнений.

Рассмотрим систему:

Расширенной матрицей системы (1) называется матрица вида:

Метод Гаусса – это метод последовательного исключения неизвестных из уравнений системы, начиная со второго уравнения по m – тое уравнение.

При этом путем элементарных преобразований матрица системы приводится к треугольной (если m = n и определитель системы ≠ 0) или ступенчатой (если m < n ) форме.

Затем, начиная с последнего по номеру уравнения, находятся все неизвестные.

Алгоритм метода Гаусса:

1) Составить расширенную матрицу системы, включающую столбец свободных членов.

2) Если а 11  0, то первую строку делим на а 11 и умножаем на (– a 21) и прибавляем вторую строку. Аналогично дойти до m –той строки:

I стр. делим на а 11 и умножаем на (– а m 1) и прибавляем m – тую стр.

При этом из уравнений, начиная со второго по m – тое, исключится переменная x 1 .

3) На 3 ‒ м шаге вторая строка используется для аналогичных элементарных преобразований строк с 3 ‒ й по m – тую. При этом исключится переменная x 2 , начиная с 3 ‒ й строки по m – тую, и т. д.

В результате этих преобразований система приведется к треугольной или ступенчатой форме (в случае треугольной формы под главной диагональю нули).

Приведение системы к треугольной или ступенчатой форме называется прямым ходом метода Гаусса , а нахождение неизвестных из полученной системы называется обратным ходом .

Пример:

Прямой ход. Приведём расширенную матрицу системы

с помощью элементарных преобразований к ступенчатому виду. Переставим первую и вторую строки матрицыA b , получим матрицу:

Сложим вторую строку полученной матрицы с первой, умноженной на (‒2), а её третью строку – с первой строкой, умноженной на (‒7). Получим матрицу

К третьей строке полученной матрицы прибавим вторую строку, умноженную на (‒3), в результате чего получим ступенчатую матрицу

Таким образом, мы привели данную систему уравнений к ступенчатому виду:

,

Обратный ход. Начиная с последнего уравнения полученной ступенчатой системы уравнений, последовательно найдём значения неизвестных:

Следующие три операции называют элементарными преобразованиями строк матрицы :

1) Умножение i-й строки матрицы на число λ ≠ 0:

которое будем записывать в виде (i) → λ(i).

2) Перестановка двух строк в матрице, например i-й и k-й строк:

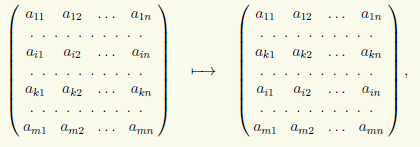
которую будем записывать в виде (i) ↔ (k).

3) Добавление к i-й строке матрицы ее k-й строки с коэффициентом λ:

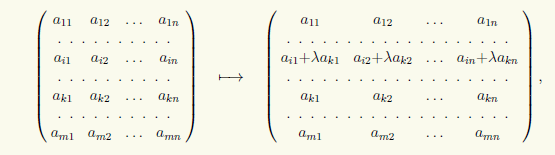
что будем записывать в виде (i) → (i) + λ(k).

Аналогичные операции над столбцами матрицы называют элементарными преобразованиями столбцов .

Каждое элементарное преобразование строк или столбцов матрицы имеет обратное элементарное преобразование , которое преобразованную матрицу превращает в исходную. Например, обратным преобразованием для перестановки двух строк является перестановка тех же строк.

Каждое элементарное преобразование строк (столбцов) матрицы А можно трактовать как умножение A слева (справа) на матрицу специального вида. Эта матрица получается, если то же преобразование выполнить над единичной матрицей . Рассмотрим подробнее элементарные преобразования строк.

Пусть матрица B получается в результате умножения i-й строки матрицы A типа m×n на число λ ≠ 0. Тогда B = Е i (λ)А, где матрица Е i (λ) получается из единичной матрицы E порядка m умножением ее i-й строки на число λ.

Пусть матрица B получается в результате перестановки i-й и k-й строк матрицы А типа m×n. Тогда B = F ik А, где матрица F ik получается из единичной матрицы E порядка m перестановкой ее i-й и k-й строк.

Пусть матрица B получается в результате добавления к i-й строке матрицы А типа m×n ее k-й строки с коэффициентом λ. Тогда B = G ik (λ)А, где матрица G ik получается из единичной матрицы E порядка m в результате добавления к i-й строке k-й строки с коэффициентом λ, т.е. на пересечении i-й строки и k-го столбца матрицы E нулевой элемент заменен на число λ.

Точно так же реализуются элементарные преобразования столбцов матрицы A, но при этом она умножается на матрицы специального вида не слева, а справа.

С помощью алгоритмов, которые основаны на элементарных преобразованиях строк и столбцов, матрицы можно преобразовывать к различному виду. Один из важнейших таких алгоритмов составляет основу доказательства следующей теоремы.

Теорема 10.1. С помощью элементарных преобразований строк любую матрицу можно привести к ступенчатому виду .

◄ Доказательство теоремы состоит в построении конкретного алгоритма приведения матрицы к ступенчатому виду. Этот алгоритм состоит в многократном повторении в определенном порядке трех операций, связанных с некоторым текущим элементом матрицы, который выбирается исходя из расположения в матрице. На первом шаге алгоритма в качестве текущего элемента матрицы выбираем верхний левый, т.е. [A] 11 .

1*. Если текущий элемент равен нулю, переходим к операции 2*. Если же он не равен нулю, то строку, в которой расположен текущий элемент (текущую строку), добавляем с соответствующими коэффициентами к строкам, расположенным ниже, так, чтобы все элементы матрицы, стоящие в столбце под текущим элементом, обратились в нуль. Например, если текущий элемент есть [A] ij , то в качестве коэффициента для k-й строки, k = i + 1, ... , нам следует взять число - [A] kj /[A] ij . Выбираем новый текущий элемент, смещаясь в матрице на один столбец вправо и на одну строку вниз, и переходим к следующему шагу, повторяя операцию 1*. Если такое смещение невозможно, т.е. достигнут последний столбец или строка, преобразования прекращаем.

2*. Если текущий элемент в некоторой строке матрицы равен нулю, то просматриваем элементы матрицы, расположенные в столбце под текущим элементом. Если среди них нет ненулевых, переходим к операции 3*. Пусть в k-й строке под текущим элементом находится ненулевой элемент. Меняем местами текущую и k-ю строки и возвращаемся к операции 1*.

3*. Если текущий элемент и все элементы под ним (в том же столбце) равны нулю, меняем текущий элемент, смещаясь в матрице на один столбец вправо. Если такое смещение возможно, т. е. текущий элемент находится не в самом правом столбце матрицы, то повторяем операцию 1* . Если же мы уже достигли правого края матрицы и смена текущего элемента невозможна, то матрица имеет ступенчатый вид, и мы можем прекратить преобразования.

Так как матрица имеет конечные размеры , а за один шаг алгоритма положение текущего элемента смещается вправо хотя бы на один столбец, процесс преобразований закончится, причем не более чем за n шагов (n - количество столбцов в матрице). Значит, наступит момент, когда матрица будет иметь ступенчатый вид.

Пример 10.10. Преобразуем матрицу к ступенчатому виду с помощью элементарных преобразований строк.

Используя алгоритм из доказательства теоремы 10.1 и записывая матрицы после окончания выполнения его операций, получаем

Элементарные преобразования матрицы - это такие преобразования матрицы , в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений , которую представляет эта матрица.

Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.

Определение

Элементарными преобразованиями строк называют:

В некоторых курсах линейной алгебры перестановка строк матрицы не выделяется в отдельное элементарное преобразование в силу того, что перестановку местами любых двух строк матрицы можно получить, используя умножение любой строки матрицы на константу k {\displaystyle k} , и прибавление к любой строке матрицы другой строки, умноженной на константу k {\displaystyle k} , k ≠ 0 {\displaystyle k\neq 0} .

Аналогично определяются элементарные преобразования столбцов .

Элементарные преобразования обратимы .

Обозначение указывает на то, что матрица A {\displaystyle A} может быть получена из B {\displaystyle B} путём элементарных преобразований (или наоборот).

Свойства

Инвариантность ранга при элементарных преобразованиях

Теорема (об инвариантности ранга при элементарных преобразованиях). Если A ∼ B {\displaystyle A\sim B} , то r a n g A = r a n g B {\displaystyle \mathrm {rang} A=\mathrm {rang} B} .

Эквивалентность СЛАУ при элементарных преобразованиях

Назовём элементарными преобразованиями над системой линейных алгебраических уравнений :

• перестановку уравнений;
• умножение уравнения на ненулевую константу;
• сложение одного уравнения с другим, умноженным на некоторую константу.

То есть элементарные преобразования над её расширенной матрицей. Тогда справедливо следующее утверждение: Напомним, что две системы называются эквивалентными, если множества их решений совпадают.

Нахождение обратных матриц

Теорема (о нахождении обратной матрицы). Пусть определитель матрицы A n × n {\displaystyle A_{n\times n}} не равен нулю, пусть матрица B {\displaystyle B} определяется выражением B = [ A | E ] n × 2 n {\displaystyle B=_{n\times 2n}} . Тогда при элементарном преобразовании строк матрицы A {\displaystyle A} к единичной матрице E {\displaystyle E} в составе B {\displaystyle B} одновременно происходит преобразование E {\displaystyle E} к A − 1 {\displaystyle A^{-1}} .